|
finitediff
|
|
finitediff
|
#include "SNpermutation.h"#include "SNgaussian.h"#include "SNmultiGaussian.h"#include "SNidentity.h"#include "SNlowerTriangular.h"#include "SNupperTriangular.h"#include "MathUtilities.h"#include "../exceptions/SNexceptions.cpp"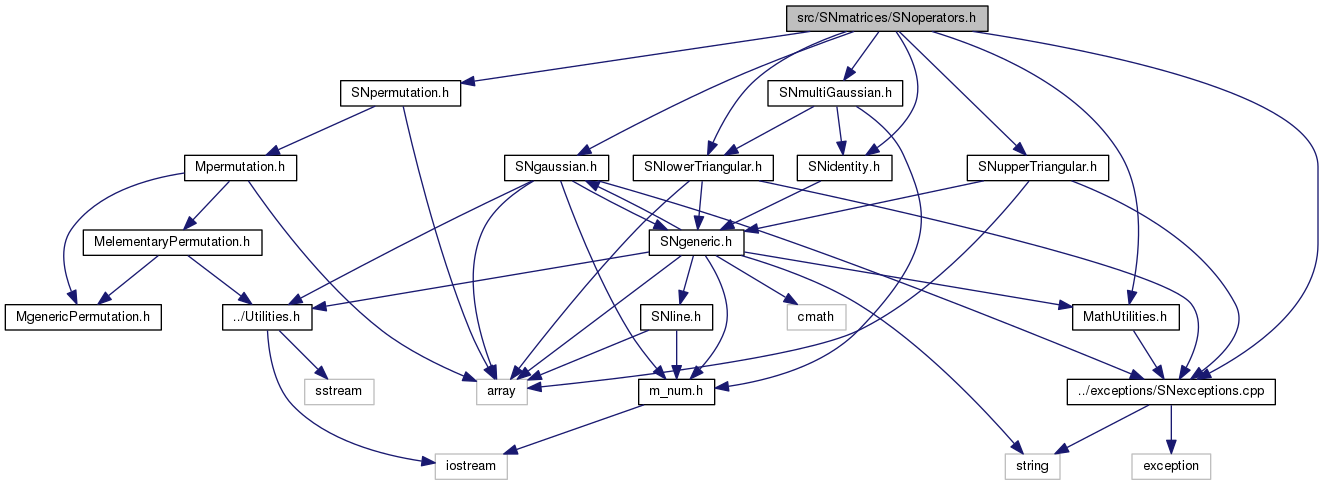
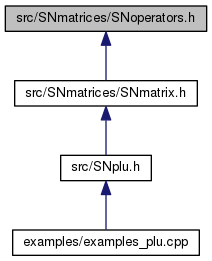
Go to the source code of this file.
Functions | |
| template<class U , class V , unsigned int s, unsigned int t> | |
| SNmatrix< U, s > | operator* (const SNgeneric< U, s > &A, const SNgeneric< V, t > &B) |
SNgeneric * SNgeneric. More... | |
| template<class U , class V , unsigned int s, unsigned int t> | |
| SNmatrix< U, s > | operator* (const SNgaussian< U, s > &A, const SNgeneric< V, t > &B) |
Product SNgaussian * SNgeneric More... | |
| template<class U , class V , unsigned int s, unsigned int t> | |
| SNmultiGaussian< U, s > | operator* (const SNgaussian< U, s > &A, const SNgaussian< V, t > &B) |
| template<class U , class V , unsigned int s, unsigned int t> | |
| SNmultiGaussian< U, s > | operator* (const SNmultiGaussian< U, s > &M, const SNgaussian< V, t > &G) |
| template<class U , class V , unsigned int s, unsigned int t> | |
| SNmatrix< U, s > | operator* (const SNmultiGaussian< U, s > &M, const SNgeneric< V, t > &E) |
Product SNmultiGaussian * SNgeneric More... | |
| template<class U , class V , unsigned int s, unsigned int t> | |
| SNmultiGaussian< U, s > | operator* (const SNmultiGaussian< U, s > &A, const SNmultiGaussian< V, t > &B) |
| template<class U , class V , unsigned int s, unsigned int t> | |
| SNlowerTriangular< U, s > | operator* (const SNgaussian< U, s > &A, const SNlowerTriangular< V, t > &B) |
| template<class U , class V , unsigned int s, unsigned int t> | |
| SNmultiGaussian< U, s > | operator* (const SNgaussian< U, s > &G, const SNmultiGaussian< V, t > &M) |
Product SNgaussian * SNmultiGaussian More... | |
| template<unsigned int tp_size> | |
| Mpermutation< tp_size > | operator* (const Mpermutation< tp_size > &p1, const Mpermutation< tp_size > &p2) |
| template<unsigned int tp_size> | |
| Mpermutation< tp_size > | operator* (const MgenericPermutation< tp_size > &A, const MgenericPermutation< tp_size > &B) |
Product MgenericPermutation * MgenericPermutation More... | |
| template<class U , unsigned int s, class V , unsigned int t> | |
| SNmatrix< U, s > | operator+ (const SNmatrix< U, s > &A, const SNmatrix< V, t > &B) |
| template<class U , unsigned int s, class V , unsigned int t> | |
| SNmatrix< U, s > | operator- (const SNgeneric< U, s > &A, const SNidentity< V, t > &B) |
| template<class U , unsigned int s, class V , unsigned int t> | |
| bool | operator== (const SNgeneric< U, s > &A, const SNgeneric< V, t > &B) |
| template<class U , unsigned int s, class V , unsigned int t> | |
| bool | operator== (const SNmatrix< U, s > &A, const SNmatrix< V, t > &B) |
| template<class U , unsigned int s, class V , unsigned int t> | |
| bool | operator== (const SNmatrix< U, s > &A, const SNupperTriangular< V, t > &B) |
| template<unsigned int tp_size> | |
| bool | operator== (const Mpermutation< tp_size > &A, const Mpermutation< tp_size > &B) |
| Return true if the two permutations are equal. More... | |
| template<unsigned int tp_size> | |
| bool | operator== (const MgenericPermutation< tp_size > &A, const MgenericPermutation< tp_size > &B) |
| Return true if the two permutations are equal. More... | |
| SNmatrix<U,s> operator* | ( | const SNgeneric< U, s > & | A, |
| const SNgeneric< V, t > & | B | ||
| ) |
In general, I cannot do better than compute everything.
The very point of making many different classes is NOT to use this 'default' implementation for the product.
When this product is used, a warning is displayed.
tooGenericWarning | SNmatrix<U,s> operator* | ( | const SNgaussian< U, s > & | A, |
| const SNgeneric< V, t > & | B | ||
| ) |
Product SNgaussian * SNgeneric
As far as the template parameters are concerned, the answer is SNmatrix<T,tp_size> with
T is the type of the gaussian (the left operand)tp_size is the common size of the two matrices.Let 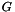 be gaussian with non trivial column
be gaussian with non trivial column 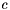 and
and 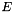 be generic. For the product
be generic. For the product 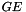 one can copy the first
one can copy the first 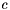 lines.
lines.
For the other lines ( 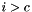 ) the sum
) the sum 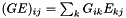 is non vanishing only with
is non vanishing only with 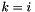 and
and 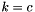 .
.
| SNmultiGaussian<U,s> operator* | ( | const SNgaussian< U, s > & | A, |
| const SNgaussian< V, t > & | B | ||
| ) |
| SNmultiGaussian<U,s> operator* | ( | const SNmultiGaussian< U, s > & | M, |
| const SNgaussian< V, t > & | G | ||
| ) |
| SNmatrix<U,s> operator* | ( | const SNmultiGaussian< U, s > & | M, |
| const SNgeneric< V, t > & | E | ||
| ) |
Product SNmultiGaussian * SNgeneric
As far as the template parameters are concerned, the answer is SNmatrix<T,tp_size> with
T is the type of the multi-gaussian (the left operand)tp_size is the common size of the two matrices.We populate the answer line by line. Let 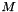 be a multi-gaussian and
be a multi-gaussian and 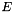 a generic matrix. We denote by
a generic matrix. We denote by 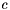 the last non-trivial column of
the last non-trivial column of 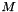 .
.
For computing 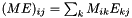 :
:
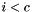 we compute the product with the first
we compute the product with the first  elements, and add the
elements, and add the 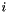 th.
th.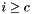 we compute the first
we compute the first  products and add the
products and add the 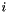 th.
th. | SNmultiGaussian<U,s> operator* | ( | const SNmultiGaussian< U, s > & | A, |
| const SNmultiGaussian< V, t > & | B | ||
| ) |
| SNlowerTriangular<U,s> operator* | ( | const SNgaussian< U, s > & | A, |
| const SNlowerTriangular< V, t > & | B | ||
| ) |
| SNmultiGaussian<U,s> operator* | ( | const SNgaussian< U, s > & | G, |
| const SNmultiGaussian< V, t > & | M | ||
| ) |
Product SNgaussian * SNmultiGaussian
The answer is SNmultiGaussian<T,tp_size> with
T is the type of the gaussian (the left operand)tp_size is the common size of the two matrices.Let 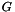 be a gaussian matrix for the column
be a gaussian matrix for the column 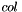 and
and 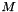 a multi-gaussian with max column
a multi-gaussian with max column 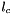 .
.
For computing the element 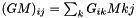 we use the structure of
we use the structure of 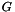 .
.
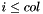 we have
we have 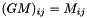 . So we copy the first
. So we copy the first 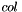 lines.
lines.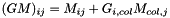 .
. | Mpermutation<tp_size> operator* | ( | const Mpermutation< tp_size > & | p1, |
| const Mpermutation< tp_size > & | p2 | ||
| ) |
The multiplication "permutation1 * permutation2" is the composition.
| Mpermutation<tp_size> operator* | ( | const MgenericPermutation< tp_size > & | A, |
| const MgenericPermutation< tp_size > & | B | ||
| ) |
Product MgenericPermutation * MgenericPermutation
The product is the composition.
This product defines the products of Mpermutation and MelementaryPermutation (there are 4 possibilities).
| SNmatrix<U,s> operator+ | ( | const SNmatrix< U, s > & | A, |
| const SNmatrix< V, t > & | B | ||
| ) |
Sum of two SNmatrix.
The return type is the one of the left argument. THUS : this is not totally commutative. You may have 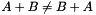
| SNmatrix<U,s> operator- | ( | const SNgeneric< U, s > & | A, |
| const SNidentity< V, t > & | B | ||
| ) |
| bool operator== | ( | const SNgeneric< U, s > & | A, |
| const SNgeneric< V, t > & | B | ||
| ) |
| bool operator== | ( | const SNmatrix< U, s > & | A, |
| const SNmatrix< V, t > & | B | ||
| ) |
| bool operator== | ( | const SNmatrix< U, s > & | A, |
| const SNupperTriangular< V, t > & | B | ||
| ) |
| bool operator== | ( | const Mpermutation< tp_size > & | A, |
| const Mpermutation< tp_size > & | B | ||
| ) |
Return true if the two permutations are equal.
| bool operator== | ( | const MgenericPermutation< tp_size > & | A, |
| const MgenericPermutation< tp_size > & | B | ||
| ) |
Return true if the two permutations are equal.
 1.8.11
1.8.11