phystricks.src.SegmentGraph.SegmentGraph Class Reference

Inheritance diagram for phystricks.src.SegmentGraph.SegmentGraph:

Collaboration diagram for phystricks.src.SegmentGraph.SegmentGraph:

Public Member Functions
def	__init__ (self, A, B)
def	Dx (self)
def	Dy (self)
def	slope (self)
def	independent (self)
def	get_point (self, x)
def	is_vertical (self)
def	is_horizontal (self)
def	equation (self)
def	length (self)
def	exact_length (self)
def	advised_mark_angle (self, pspict=None)
def	phyFunction (self)
def	symmetric_by (self, O)
def	inside_bounding_box (self, bb=None, xmin=None, xmax=None, ymin=None, ymax=None)
def	segment (self, projection=False)
def	fit_inside (self, xmin, xmax, ymin, ymax)
def	parametric_curve (self)
def	copy (self)
def	get_regular_points (self, dx)
def	get_wavy_points (self, dx, dy)
def	get_point_length (self, d, advised=True)
def	get_point_proportion (self, p, advised=True)
def	put_arrow (self, position=0.5, size=0.01, pspict=None)
def	put_measure (self, measure_distance, mark_distance, mark_angle=None, text="", position=None, pspict=None, pspicts=None)
def	get_measure (self, measure_distance, mark_distance, mark_angle=None, text=None, position=None, pspict=None, pspicts=None)
def	put_code (self, n=1, d=0.1, l=0.1, angle=45, pspict=None, pspicts=None)
def	get_code (self, n=1, d=0.1, l=0.1, angle=45, pspict=None, pspicts=None)
def	get_divide_in_two (self, n=1, d=0.1, l=0.1, angle=45\, pspict=None, pspicts=None)
def	divide_in_two (self, n=1, d=0.1, l=0.1, angle=45, pspict=None, pspicts=None)
def	Point (self)
def	midpoint (self, advised=True)
def	AffineVector (self)
def	get_normal_vector (self, origin=None)
def	get_tangent_vector (self)
def	polaires (self)
def	angle (self)
def	direction (self)
def	projection (self, segment, advised=False)
def	bisector (self, code=None)
def	orthogonal (self, point=None)
def	orthogonal_trough (self, P)
def	parallel_trough (self, P)
def	is_orthogonal (self, other)
	Return true is self and other are orthogonal segments. More...
def	is_almost_orthogonal (self, other, epsilon=0.001)
	Return true is self and other are orthogonal segments. More...
def	translate (self, a, b=None)
	translate the segment with the given vector More...
def	fix_origin (self, a, b=None)
def	inverse (self)
def	rotation (self, angle)
def	get_visual_length (self, xunit=None, yunit=None, pspict=None)
def	fix_visual_size (self, l, xunit=None, yunit=None, pspict=None)
def	add_size_extremity (self, l)
def	fix_size (self, l, only_F=False, only_I=False)
def	add_size (self, lI=0, lF=0)
def	dilatation (self, coef)
def	dilatationI (self, coef)
def	dilatationF (self, coef)
def	normalize (self, l=1)
def	graph (self, mx=None, Mx=None)
def	default_associated_graph_class (self)
def	__mul__ (self, coef)
def	translation (self, v)
def	__add__ (self, other)
def	__eq__ (self, other)
	Says if two segments are equal. More...
def	__sub__ (self, other)
def	__rmul__ (self, coef)
def	__neg__ (self)
def	__div__ (self, coef)
def	__div__ (self, coef)
def	__str__ (self)
def	mark_point (self, pspict=None)
def	representative_points (self)
def	latex_code (self, language=None, pspict=None)
def	tikz_code (self, pspict=None)

Public Attributes
	I
	F
	measure
	coefs
	slope

Private Member Functions
def	_bounding_box (self, pspict)
def	_math_bounding_box (self, pspict=None)

Constructor & Destructor Documentation

def phystricks.src.SegmentGraph.SegmentGraph.__init__	(		self,
			A,
			B
	)

Member Function Documentation

def phystricks.src.SegmentGraph.SegmentGraph.__add__	(		self,
			other
	)

If the other is a vector, return the translated segment

INPUT:
- ``other`` - an other segment

OUTPUT:
A new  segment that has the same origin as `self`.

EXAMPLES::

    sage: from phystricks import *
    sage: a=Vector(1,1)
    sage: b=Vector(2,3)
    sage: print a+b
    <vector I=<Point(0,0)> F=<Point(3,4)>>

def phystricks.src.SegmentGraph.SegmentGraph.__div__	(		self,
			coef
	)

def phystricks.src.SegmentGraph.SegmentGraph.__div__	(		self,
			coef
	)

def phystricks.src.SegmentGraph.SegmentGraph.__eq__	(		self,
			other
	)

Says if two segments are equal.

Two segments are equal when their initial and final points are equal

def phystricks.src.SegmentGraph.SegmentGraph.__mul__	(		self,
			coef
	)

multiply the segment by a coefficient.

INPUT:
- ``coef`` - the multiplying coefficient

OUTPUT:
A new segment.

EXAMPLES::

    sage: s=Segment(Point(1,1),Point(2,2))
    sage: print 3*s
    <segment I=<Point(1,1)> F=<Point(4,4)>>

The initial point stays the same (this is not the same behaviour as in self.normalize !)

def phystricks.src.SegmentGraph.SegmentGraph.__neg__

(

self

)

def phystricks.src.SegmentGraph.SegmentGraph.__rmul__	(		self,
			coef
	)

def phystricks.src.SegmentGraph.SegmentGraph.__str__

(

self

)

def phystricks.src.SegmentGraph.SegmentGraph.__sub__	(		self,
			other
	)

def phystricks.src.SegmentGraph.SegmentGraph._bounding_box (   self,   pspict  )

private

def phystricks.src.SegmentGraph.SegmentGraph._math_bounding_box (   self,   pspict = None  )

private

def phystricks.src.SegmentGraph.SegmentGraph.add_size	(		self,
			lI = 0,
			lF = 0
	)

Return a new Segment with extra length lI at the initial side and lF at the final side. 

def phystricks.src.SegmentGraph.SegmentGraph.add_size_extremity	(		self,
			l
	)

Add a length <l> at the extremity of the segment. Return a new object.

def phystricks.src.SegmentGraph.SegmentGraph.advised_mark_angle	(		self,
			pspict = None
	)

def phystricks.src.SegmentGraph.SegmentGraph.AffineVector

(

self

)

def phystricks.src.SegmentGraph.SegmentGraph.angle

(

self

)

return the angle of the segment.

This is the angle between the segment and the horizontal axe. 
The returned angle is positive.

EXAMPLES::

    sage: from phystricks import *
    sage: S=Segment(Point(1,1),Point(2,2))
    sage: type(S.angle())
    <class 'phystricks.SmallComputations.AngleMeasure'>
    sage: S.angle().degree
    45
    sage: S.angle().radian
    1/4*pi

    sage: S=Segment(Point(1,1),Point(2,0))
    sage: S.angle().degree
    315

def phystricks.src.SegmentGraph.SegmentGraph.bisector	(		self,
			code = None
	)

return the segment which is orthogonal to the center of 'self'.

def phystricks.src.SegmentGraph.SegmentGraph.copy

(

self

)

def phystricks.src.SegmentGraph.SegmentGraph.default_associated_graph_class

(

self

)

Return the class which is the Graph associated type

def phystricks.src.SegmentGraph.SegmentGraph.dilatation	(		self,
			coef
	)

Return a Segment which is dilated by the coefficient coef 

    This adds the same length at both extremities.
    The segment A --> B dilated by 0.5 returns
    a segment C --> D where [CD] is the _central_ half of [AB].
    If you want to add some length to one
    of the extremities, use
    self.add_size
    or
    l*self
    with a scalar l.

INPUT:
- ``coef`` - a number. This is the dilatation coefficient

OUTPUT:
a new segment

EXAMPLES::

    sage: from phystricks import *
    sage: S=Segment(Point(-2,-2),Point(2,2))
    sage: print S.dilatation(0.5)           
    <segment I=<Point(-1.00000000000000,-1.00000000000000)> F=<Point(1.00000000000000,1.00000000000000)>>

But ::

    sage: v=AffineVector(Point(-2,-2),Point(2,2))
    sage: print v.dilatation(0.5)                
    <vector I=<Point(-2,-2)> F=<Point(0.000000000000000,0.000000000000000)>>

def phystricks.src.SegmentGraph.SegmentGraph.dilatationF	(		self,
			coef
	)

return a dilated segment, but only enlarges at the final extremity.

def phystricks.src.SegmentGraph.SegmentGraph.dilatationI	(		self,
			coef
	)

return a dilated segment, but only enlarges at the initial extremity.

def phystricks.src.SegmentGraph.SegmentGraph.direction

(

self

)

def phystricks.src.SegmentGraph.SegmentGraph.divide_in_two	(		self,
			n = 1,
			d = 0.1,
			l = 0.1,
			angle = 45,
			pspict = None,
			pspicts = None
	)

def phystricks.src.SegmentGraph.SegmentGraph.Dx

(

self

)

def phystricks.src.SegmentGraph.SegmentGraph.Dy

(

self

)

def phystricks.src.SegmentGraph.SegmentGraph.equation

(

self

)

return the equation of the line under the form
x + by + c = 0

Coefficients 'b' and 'c' are numerical approximations. 
See Utilities.Intersection

EXAMPLES::

    sage: from phystricks import *
    sage: Segment(Point(0,0),Point(1,1)).equation
    x - y == 0
    sage: Segment(Point(1,0),Point(0,1)).equation
    x + y - 1 == 0

def phystricks.src.SegmentGraph.SegmentGraph.exact_length

(

self

)

return the length of the segment.

def phystricks.src.SegmentGraph.SegmentGraph.fit_inside	(		self,
			xmin,
			xmax,
			ymin,
			ymax
	)

return the largest segment that fits into the given bounds

def phystricks.src.SegmentGraph.SegmentGraph.fix_origin	(		self,
			a,
			b = None
	)

Return the segment fixed at `P`. This is the translation
of `self`  by `P-self`.  In other words, it returns the
segment which is parallel to self trough the given point.

Typically it is used in the framework of affine vector..

INPUT:

- ``P`` - The point on which we want to "attach" the new segment.

or 

- two numbers that are the coordinates of the "attach" point.

OUTPUT:

A new segment (or vector) with initial point at `P`

EXAMPLES:
    
We can fix the origin by giving the coordinates of the new origin::

    sage: from phystricks import *
    sage: v=AffineVector( Point(1,1),Point(2,2) )
    sage: w=v.fix_origin(3,5)
    sage: w.I.coordinates(),w.F.coordinates()
    ('(3,5)', '(4,6)')

We can also give a point::    

    sage: P=Point(-1,-pi)
    sage: u=w.fix_origin(P)
    sage: u.I.coordinates(),u.F.coordinates()
    ('(-1,-pi)', '(0,-pi + 1)')

def phystricks.src.SegmentGraph.SegmentGraph.fix_size	(		self,
			l,
			only_F = False,
			only_I = False
	)

return a new segment with size l.

This function has not to be used by the end user. 
Use self.normalize() instead.

def phystricks.src.SegmentGraph.SegmentGraph.fix_visual_size	(		self,
			l,
			xunit = None,
			yunit = None,
			pspict = None
	)

return a segment with the same initial point, but with visual length  `l`

def phystricks.src.SegmentGraph.SegmentGraph.get_code	(		self,
			n = 1,
			d = 0.1,
			l = 0.1,
			angle = 45,
			pspict = None,
			pspicts = None
	)

def phystricks.src.SegmentGraph.SegmentGraph.get_divide_in_two	(		self,
			n = 1,
			d = 0.1,
			l = 0.1,
			angle = 45\,
			pspict = None,
			pspicts = None
	)

def phystricks.src.SegmentGraph.SegmentGraph.get_measure	(		self,
			measure_distance,
			mark_distance,
			mark_angle = None,
			text = None,
			position = None,
			pspict = None,
			pspicts = None
	)

The difference between 'put_measure' and 'get_measure'
is that 'get_measure' returns the measure graph while
'put_measure' adds the measure graph to the segment.

This allows constructions like
mesL=Segment(F,D).get_measure(-0.2,0.1,90,"\( 10\)",pspict=pspict,position="S")
and then draw mesL. The Segment(F,D) object is not drawn.

If 'mark_angle' is 'None', then the angle
will be perpendicular to 'self'

def phystricks.src.SegmentGraph.SegmentGraph.get_normal_vector	(		self,
			origin = None
	)

returns a normalized normal vector at the center of the segment

- `origin` (optional). If given, the vector will 
    be attached to that point.

def phystricks.src.SegmentGraph.SegmentGraph.get_point	(		self,
			x
	)

Return the point of abscisses 'x' on the line.

def phystricks.src.SegmentGraph.SegmentGraph.get_point_length	(		self,
			d,
			advised = True
	)

Return a point on the segment at distance 'd' from the initial point (in the direction of the final point)

def phystricks.src.SegmentGraph.SegmentGraph.get_point_proportion	(		self,
			p,
			advised = True
	)

Return a point on the segment which is at the position
(p-1)*I+p*F
if I and F denote the initial and final point of the segment.

def phystricks.src.SegmentGraph.SegmentGraph.get_regular_points	(		self,
			dx
	)

Notice that it does not return the last point of the segment, unless the length is a multiple of dx.
   this is why we add by hand the last point in GetWavyPoint

def phystricks.src.SegmentGraph.SegmentGraph.get_tangent_vector

(

self

)

return a tangent vector at center of the segment

def phystricks.src.SegmentGraph.SegmentGraph.get_visual_length	(		self,
			xunit = None,
			yunit = None,
			pspict = None
	)

Return the visual length of self. That is the length
taking xunit and  yunit into account

def phystricks.src.SegmentGraph.SegmentGraph.get_wavy_points	(		self,
			dx,
			dy
	)

Return a list of points that make a wave around the segment.
The wavelength is dx and the amplitude is dy.
The first and the last points are self.I and self.F and are then *on* the segment. Thus the wave begins and ends on the segment.

def phystricks.src.SegmentGraph.SegmentGraph.graph	(		self,
			mx = None,
			Mx = None
	)

def phystricks.src.SegmentGraph.SegmentGraph.independent

(

self

)

return the b in the equation
y = ax + b

If the line is vertical, raise an ZeroDivisionError

EXAMPLES::

    sage: from phystricks import *
    sage: s = Segment(Point(0,3),Point(6,-1))
    sage: s.independent
    3

sage: Segment(Point(1,2),Point(-1,1)).independent
3/2

def phystricks.src.SegmentGraph.SegmentGraph.inside_bounding_box	(		self,
			bb = None,
			xmin = None,
			xmax = None,
			ymin = None,
			ymax = None
	)

Return a segment that is the part of self contained inside the given bounding box.

def phystricks.src.SegmentGraph.SegmentGraph.inverse

(

self

)

Return the segment BA instead of AB.

Not to be confused with (-self). The latter is a rotation
of 180 degree of self.

def phystricks.src.SegmentGraph.SegmentGraph.is_almost_orthogonal	(		self,
			other,
			epsilon = 0.001
	)

Return true is self and other are orthogonal segments.

The answer is based on numerical approximations of the slopes. If 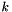is the slope of self, check if the slope of the other is 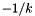up to epsilon.

See also

is_orthogonal

def phystricks.src.SegmentGraph.SegmentGraph.is_horizontal

(

self

)

def phystricks.src.SegmentGraph.SegmentGraph.is_orthogonal	(		self,
			other
	)

Return true is self and other are orthogonal segments.

The answer is exact, so you can be surprised if some numerical approximations were made before.

See also

is_almost_orthogonal

def phystricks.src.SegmentGraph.SegmentGraph.is_vertical

(

self

)

def phystricks.src.SegmentGraph.SegmentGraph.latex_code	(		self,
			language = None,
			pspict = None
	)

def phystricks.src.SegmentGraph.SegmentGraph.length

(

self

)

return (a numerical approximation of) the length of the segment

EXAMPLES::

    sage: from phystricks import *
    sage: Segment(Point(1,1),Point(2,2)).length
    sqrt(2)

def phystricks.src.SegmentGraph.SegmentGraph.mark_point	(		self,
			pspict = None
	)

return the point on which a mark has to be placed
if we use the method put_mark.  
If we have a segment, the mark is at center 

def phystricks.src.SegmentGraph.SegmentGraph.midpoint	(		self,
			advised = True
	)

def phystricks.src.SegmentGraph.SegmentGraph.normalize	(		self,
			l = 1
	)

Normalize the segment to <l> by dilating in both extremities

NOTES:
* If self is of length zero, return a copy of self.
* If not length is given, normalize to 1.
* If the given new length is negative, 
    if self is a segment, consider the absolute value

INPUT:
- ``l`` - (default=1) a number, the new length

OUTPUT:
A segment or a vector

EXAMPLES::

    sage: from phystricks import *
    sage: s=Segment(Point(0,0),Point(1,0))
    sage: print s.normalize(2)
    <segment I=<Point(-0.5,0)> F=<Point(1.5,0)>>
    sage: print s.normalize(-1)
    <segment I=<Point(0,0)> F=<Point(1,0)>>

def phystricks.src.SegmentGraph.SegmentGraph.orthogonal	(		self,
			point = None
	)

return the segment with a rotation of 90 degree.
The new segment is, by default, still attached to the same point.

If 'point' is given, the segment will be attached to that point

Not to be confused with self.get_normal_vector

def phystricks.src.SegmentGraph.SegmentGraph.orthogonal_trough	(		self,
			P
	)

return a segment orthogonal to self passing trough P.

The starting point is 'P' and the final point is the 
intersection with 'self'

If these two points are the same --when d^2(P,Q)<0.001 
(happens when 'P' belongs to 'self'), the end point is not guaranteed.

By the way, when you want
Segment(A,B).orthogonal_trough(B)
you can use
seg=Segment(B,A).orthogonal()
instead.

def phystricks.src.SegmentGraph.SegmentGraph.parallel_trough	(		self,
			P
	)

return a segment parallel to self passing trough P

def phystricks.src.SegmentGraph.SegmentGraph.parametric_curve

(

self

)

Return the parametric curve corresponding to `self`.

The starting point is `self.I` and the parameters is the arc length.
The parameter is positive on the side of `self.B` and negative on the
opposite side.

EXAMPLES::

    sage: from phystricks import *
    sage: segment=Segment(Point(0,0),Point(1,1))
    sage: curve=segment.parametric_curve()
    sage: print curve(0)
    <Point(0,0)>
    sage: print curve(1)
    <Point(1/2*sqrt(2),1/2*sqrt(2))>
    sage: print curve(segment.length)
    <Point(1,1)>

def phystricks.src.SegmentGraph.SegmentGraph.phyFunction

(

self

)

def phystricks.src.SegmentGraph.SegmentGraph.Point

(

self

)

Return the point X such that as free vector, 0->X == self

More precisely, if self is the segment A->B, return the point B-A

def phystricks.src.SegmentGraph.SegmentGraph.polaires

(

self

)

def phystricks.src.SegmentGraph.SegmentGraph.projection	(		self,
			segment,
			advised = False
	)

Return the projection of self on the given segment

It also works with vectors

INPUT:
- ``segment`` - the line on which we want to project

EXAMPLES::

    sage: from phystricks import *
    sage: l = Segment(Point(0,0),Point(0,1))
    sage: v = AffineVector(Point(-1,1),Point(-2,3))
    sage: print v.equation
    x + 1/2*y + 1/2 == 0
    sage: print v.projection(l)
    <vector I=<Point(0,1)> F=<Point(0,3)>>
    sage: print l.projection(v)
    <segment I=<Point(-2/5,-1/5)> F=<Point(-4/5,3/5)>>

    sage: l = Segment(Point(0,0),Point(1,2))
    sage: s = Segment(Point(-2,1),Point(-3,4))
    sage: print s.projection(l)
    <segment I=<Point(0,0)> F=<Point(1,2)>>

def phystricks.src.SegmentGraph.SegmentGraph.put_arrow	(		self,
			position = 0.5,
			size = 0.01,
			pspict = None
	)

Add a small arrow at the given position. 
`position` is a number between 0 and 1.

The arrow is pointed from self.I to self.F and is by
default put at the middle of the segment.

The arrow is a vector of size (by default) 0.01. 

def phystricks.src.SegmentGraph.SegmentGraph.put_code	(		self,
			n = 1,
			d = 0.1,
			l = 0.1,
			angle = 45,
			pspict = None,
			pspicts = None
	)

add small line at the center of the segment.

'n' add 'n' small lines. Default is 1
'd' is the distance between two of them
'l' is the (visual) length of the segment
'angle' is the angle with 'self'.

def phystricks.src.SegmentGraph.SegmentGraph.put_measure	(		self,
			measure_distance,
			mark_distance,
			mark_angle = None,
			text = "",
			position = None,
			pspict = None,
			pspicts = None
	)

def phystricks.src.SegmentGraph.SegmentGraph.representative_points

(

self

)

def phystricks.src.SegmentGraph.SegmentGraph.rotation	(		self,
			angle
	)

Return the segment attached to the same point but with
a rotation of angle.

INPUT:

- ``angle`` - the value of the rotation angle (degree or AngleMeasure)

def phystricks.src.SegmentGraph.SegmentGraph.segment	(		self,
			projection = False
	)

serves to transform a vector into a segment

def phystricks.src.SegmentGraph.SegmentGraph.slope

(

self

)

return the angular coefficient of line.

This is the coefficient a in the equation
y = ax + b

This is not the same as the coefficient a in self.equation
ax + by + c == 0

of the points.

OUTPUT:
a number

EXAMPLES::

    sage: from phystricks import *
    sage: Segment(Point(0,0),Point(1,1)).slope
    1
    sage: Segment(Point(1,1),Point(0,0)).slope
    1
    sage: Segment(Point(1,2),Point(-1,8)).slope
    -3

NOTE:

If the line is vertical, raise a ZeroDivisionError

def phystricks.src.SegmentGraph.SegmentGraph.symmetric_by	(		self,
			O
	)

return a segment which is symmetric to 'self' with respect to the point 'O'

def phystricks.src.SegmentGraph.SegmentGraph.tikz_code	(		self,
			pspict = None
	)

def phystricks.src.SegmentGraph.SegmentGraph.translate	(		self,
			a,
			b = None
	)

translate the segment with the given vector

If two arguments are given, we assume that they are the coordinates of the translation vector. If only one argument is given, we assume that this is the vector.

So there are three way to use :

• with a vector :

  segment.tranlate(v)

• With two numbers :

  segment.tranlate(x,y)

• With a tuple :

  v=(1,2)
  segment.translate(v)

def phystricks.src.SegmentGraph.SegmentGraph.translation	(		self,
			v
	)

Member Data Documentation

phystricks.src.SegmentGraph.SegmentGraph.coefs

phystricks.src.SegmentGraph.SegmentGraph.F

phystricks.src.SegmentGraph.SegmentGraph.I

phystricks.src.SegmentGraph.SegmentGraph.measure

phystricks.src.SegmentGraph.SegmentGraph.slope

---

The documentation for this class was generated from the following file:

• src/SegmentGraph.py