|
| def | is_real (z) |
| |
| def | test_imaginary_part (z, epsilon=0.0001) |
| |
| def | test_imaginary_part_point (P, epsilon=0.0001) |
| |
| def | distance_sq (P, Q, numerical=False) |
| | return the squared distance between P and Q More...
|
| |
| def | distance (P, Q) |
| |
| def | inner_product (v, w, numerical=False) |
| | Return the inner product of vectors v and w More...
|
| |
| def | Intersection (f, g, a=None, b=None, numerical=False) |
| | When f and g are objects with an attribute equation, return the list of points of intersections. More...
|
| |
| def | point_to_box_intersection (P, box, pspict=None) |
| | The intersection between the line from the given point and the center of the given box. More...
|
| |
| def | PointToPolaire (P=None, x=None, y=None, origin=None, numerical=True) |
| |
| def | EnsurephyFunction (f) |
| |
| def | EnsureParametricCurve (curve) |
| |
| def | check_too_large (obj, pspict=None) |
| |
| def | general_function_get_point (fun, x, advised=True) |
| |
| def | latinize (word) |
| |
| def | counterName () |
| |
| def | newlengthName () |
| |
| def | sublist (l, condition) |
| |
| def | make_psp_list (pspict, pspicts) |
| |
| def | no_symbol (arg) |
| |
| def | get_equal_lengths_code (s1, s2, n=1, d=0.1, l=0.1, angle=45, pspict=None, pspicts=None) |
| |
| def | put_equal_lengths_code (s1, s2, n=1, d=0.1, l=0.1, angle=45, pspict=None, pspicts=None) |
| |
| def | number_to_string (x, digits) |
| | turn the given number into a string with some conversion and approximations rules. More...
|
| |
| def phystricks.src.Utilities.general_function_get_point |
( |
|
fun, |
|
|
|
x, |
|
|
|
advised = True |
|
) |
| |
Return a point on the graph of the function with the given x, i.e. it return the point (x,f(x)).
Also set an attribute advised_mark_angle to the point. This angle is the normal exterior to the graph; visually this is usually the best place to put a mark. Typically you use this as
P=f.get_point(3)
P.mark(radius,P.advised_mark_angle,"$P$")
NOTE:
If you don't plan to put a mark on the point, you are invited
to use advised=False in order to speed up the computations.
| def phystricks.src.Utilities.Intersection |
( |
|
f, |
|
|
|
g, |
|
|
|
a = None, |
|
|
|
b = None, |
|
|
|
numerical = False |
|
) |
| |
When f and g are objects with an attribute equation, return the list of points of intersections.
- The list of point is sorted by order of
x coordinates.
- Return only real solutions.
Only numerical approximations are returned as there are some errors otherwise. As an example the following #solving return points that are not even near from the circle 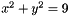 :
:
1 solve( [ -1/3*sqrt(3)*y + 1/3*sqrt(3)*(-0.19245008972987399*sqrt(3) - 3) + x == 0,x^2 + y^2 - 9 == 0 ],[x,y] )
Examples
1 sage:
from phystricks
import *
5 sage:
for P
in pts:
print P
4 sage:
for P
in pts:
print P
5 <
Point(-5.497787143782138,0.707106781186548)>
6 <
Point(-2.3561944901923466,-0.707106781186546)>
7 <
Point(0.7853981633974484,0.707106781186548)>
8 <
Point(3.926990816987241,-0.707106781186547)>
If 'numerical' is True, it search for the intersection points of the functions 'f' and 'g' (it only work with functions). In this case an interval is required.
| def phystricks.src.Utilities.latinize |
( |
|
word | ) |
|
return a "latinized" version of a string.
From a string, return something that can be used as point name, file name.
In particular, remove the special characters, put everything in lowercase,
and turn the numbers into letters.
This function is used in order to turn the script name into a
string that can be a filename for the LaTeX's intermediate file.
INPUT:
- ``word`` - string
OUTPUT:
string
EXAMPLES::
sage: from phystricks.SmallComputations import *
sage: latinize("/home/MyName/.sage/my_script11.py")
'homeMyNameDsagemyscriptOODpy'
::
sage: from phystricks.SmallComputations import *
sage: latinize("/home/MyName/.sage/my_script13.py")
'homeMyNameDsagemyscriptOThDpy'
| def phystricks.src.Utilities.number_to_string |
( |
|
x, |
|
|
|
digits |
|
) |
| |
turn the given number into a string with some conversion and approximations rules.
When one coordinate if very small (lower than 0.0001), it is rounded to zero in order to avoid string like "0.2335e-6" in the pstricks code.
The parameter digit is not the same as the one in Sage's numerical_approx. Here we compute a numerical approximation (the one of sage) and then we cut the resulting string to the desired numbers of digits. The rounding is thus not always the expected one. The reason is this kind of expression :
1 a=7.73542889062775*cos(11/9*pi + 1.30951587282752) - 7.55775391156456*cos(5/18*pi) + 2.5*cos(2/9*pi)
2 print(numerical_approx(a))
3 print(numerical_approx(a,digits=5))
The first print is deterministic (0.329851686365047), while the second one is not.
Remark : undefined behaviour is the integer part of x requires more digits than digits.
| def phystricks.src.Utilities.PointToPolaire |
( |
|
P = None, |
|
|
|
x = None, |
|
|
|
y = None, |
|
|
|
origin = None, |
|
|
|
numerical = True |
|
) |
| |
Return the polar coordinates of a point.
INPUT:
- ``P`` - (default=None) a point
- ``x,y`` - (defautl=None) the coordinates of the points
EXAMPLES:
You can provide a point::
sage: from phystricks import Point
sage: from phystricks.SmallComputations import *
sage: print PointToPolaire(Point(1,1))
PolarCoordinates, r=sqrt(2),degree=45,radian=1/4*pi
or directly the coordinates ::
sage: print PointToPolaire(x=1,y=1)
PolarCoordinates, r=sqrt(2),degree=45,radian=1/4*pi
 :
:  1.8.11
1.8.11