phystricks.src.CircleGraph.CircleGraph Class Reference

Inheritance diagram for phystricks.src.CircleGraph.CircleGraph:

Collaboration diagram for phystricks.src.CircleGraph.CircleGraph:

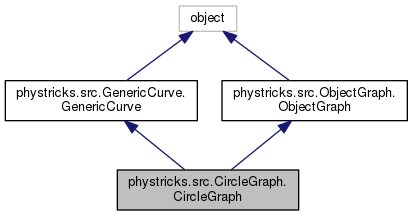
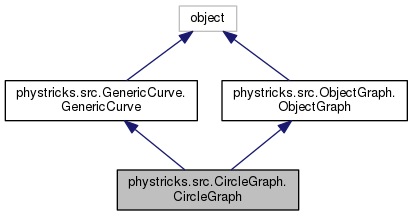
Public Member Functions
def	__init__ (self, center, radius, angleI=0, angleF=360, visual=False, pspict=None)
def	equation (self, numerical=False)
def	parametric_curve (self, a=None, b=None)
def	put_arrow (self, arg, pw)
def	getPoint (self, theta, advised=True, numerical=False)
def	get_point (self, theta, advised=True, numerical=False)
def	get_regular_points (self, mx, Mx, l=None, n=None, advised=True)
def	get_tangent_vector (self, theta)
def	get_tangent_segment (self, theta)
def	get_normal_vector (self, theta)
def	xmax (self, angleI, angleF)
def	xmin (self, angleI, angleF)
def	ymax (self, angleI, angleF)
def	ymin (self, angleI, angleF)
def	graph (self, angleI, angleF)
def	__str__ (self)
def	copy (self)
def	representative_points (self)
def	action_on_pspict (self, pspict)
Public Member Functions inherited from phystricks.src.GenericCurve.GenericCurve
def	__init__ (self, pI, pF)
def	addPlotPoint (self, x)
def	getFunctionIntegral (self, fun, lmin=None, lmax=None)
def	total_curvature (self)
def	getNextRegularFunctionParameters (self, lmin, lmax, fun, df, xunit=1, yunit=1)
def	getRegularFunctionParameters (self, lmin, lmax, fun, df, initial_point=False, final_point=False, xunit=1, yunit=1, numerical=True)
def	getRegularLengthParameters (self, mll, Mll, dl, initial_point=False, final_point=False, xunit=1, yunit=1, numerical=True)
def	getRegularCurvatureParameter (self, mll, Mll, dl, initial_point=False, final_point=False, xunit=1, yunit=1)
def	representativeParameters (self)
def	representative_points (self)
def	get_minmax_data (self, start=None, end=None)
def	xmax (self, deb, fin)
def	xmin (self, deb, fin)
def	ymax (self, deb, fin)
def	ymin (self, deb, fin)
Public Member Functions inherited from phystricks.src.ObjectGraph.ObjectGraph
def	__init__ (self, obj)
def	draw_edges (self)
def	wave (self, dx, dy)
def	get_arrow (self, llam)
def	get_mark (self, dist, angle=None, text=None, mark_point=None, added_angle=None, position=None, pspict=None)
def	put_mark (self, dist=None, angle=None, text="", mark_point=None, added_angle=None, position=None, pspict=None, pspicts=None)
	put a mark on an object More...
def	add_option (self, opt)
def	get_option (opt)
def	remove_option (opt)
def	merge_options (self, graph)
def	conclude_params (self)
def	params (self, language, refute=[])
def	bracketAttributesText (self, language, refute=[])
def	action_on_pspict (self, pspict)
def	conclude (self, pspict)
def	bounding_box (self, pspict=None)
def	math_bounding_box (self, pspict)
def	latex_code (self, pspict, language=None)

Public Attributes
	linear_plotpoints
	center
	radius
	diameter
	angleI
	angleF
	visual
	pspict
Public Attributes inherited from phystricks.src.GenericCurve.GenericCurve
	linear_plotpoints
	curvature_plotpoints
	added_plotpoints
	pI
	pF
Public Attributes inherited from phystricks.src.ObjectGraph.ObjectGraph
	obj
	parameters
	wavy
	waviness
	options
	draw_bounding_box
	already_computed_BB
	already_computed_math_BB
	record_add_to_bb
	separator_name
	in_math_bounding_box
	in_bounding_box
	added_objects
	take_BB
	take_math_BB
	mark
	marque

Private Member Functions
def	_math_bounding_box (self, pspict=None)
def	_bounding_box (self, pspict=None)

Private Attributes
	_parametric_curve
	_equation
	_numerical_equation

Detailed Description

This is a circle, or an arc of circle.

INPUT:

- ``center`` - a point, the center of the circle.

- ``radius`` - a number, the radius of the circle.

- ``self.angleI`` - (default=0) the beginning angle of the arc (degree).

- ``self.angleF`` - (default=360) the ending angle of the arc (degree).
- ``visual`` - (default=False) if 'True', the radius is taken as a 'visual' length.


OUTPUT:

A circle ready to be drawn.

EXAMPLES::

    sage: from phystricks import *
    sage: circle=Circle(Point(-1,1),3)

If you want the same circle but between the angles 45 and 78::
    
    sage: other_circle=circle.graph(45,78)

Constructor & Destructor Documentation

def phystricks.src.CircleGraph.CircleGraph.__init__	(		self,
			center,
			radius,
			angleI = 0,
			angleF = 360,
			visual = False,
			pspict = None
	)

Member Function Documentation

def phystricks.src.CircleGraph.CircleGraph.__str__

(

self

)

def phystricks.src.CircleGraph.CircleGraph._bounding_box (   self,   pspict = None  )

private

def phystricks.src.CircleGraph.CircleGraph._math_bounding_box (   self,   pspict = None  )

private

def phystricks.src.CircleGraph.CircleGraph.action_on_pspict	(		self,
			pspict
	)

def phystricks.src.CircleGraph.CircleGraph.copy

(

self

)

Return a copy of the object as geometrical object.

It only copies the center and the radius. In particular
the following are not copied:

- style of drawing.

- initial and final angle if `self` is an arc.

EXAMPLES:

Python copies by assignation::

    sage: from phystricks import *
    sage: c1=Circle( Point(1,1),2 )
    sage: c2=c1
    sage: c2.center=Point(3,3)
    sage: print c1.center
    <Point(3,3)>

The method :func:`copy` pass through::

    sage: c1=Circle( Point(1,1),3 )
    sage: c2=c1.copy()
    sage: c2.center=Point(3,3)
    sage: print c1.center
    <Point(1,1)>

NOTE:

Due to use of `lazy_attribute`, it is not recommended to change the center of
a circle after having defined it.

def phystricks.src.CircleGraph.CircleGraph.equation	(		self,
			numerical = False
	)

Return the equation of `self`.

OUTPUT:

an equation.

EXAMPLES::

    sage: from phystricks import *
    sage: circle=Circle(Point(0,0),1)
    sage: circle.equation()
    x^2 + y^2 - 1 == 0

::

    sage: circle=CircleOA(Point(-1,-1),Point(0,0))
    sage: circle.equation()
    (x + 1)^2 + (y + 1)^2 - 2 == 0

If 'numerical' is True, return numerical approximations of the coefficients.

def phystricks.src.CircleGraph.CircleGraph.get_normal_vector	(		self,
			theta
	)

Return a normal vector at the given angle 

INPUT:

- ``theta`` - an angle in degree or :class:`AngleMeasure`.

OUTPUT:

An affine vector

EXAMPLES::

    sage: from phystricks import *
    sage: C=Circle(Point(0,0),2)
    sage: print C.get_normal_vector(45)
    <vector I=<Point(sqrt(2),sqrt(2))> F=<Point(3/2*sqrt(2),3/2*sqrt(2))>>

def phystricks.src.CircleGraph.CircleGraph.get_point	(		self,
			theta,
			advised = True,
			numerical = False
	)

def phystricks.src.CircleGraph.CircleGraph.get_regular_points	(		self,
			mx,
			Mx,
			l = None,
			n = None,
			advised = True
	)

return regularly spaced points on the circle

INPUT:

- ``mx`` - initial angle (degree).
- ``Mx`` - final angle (degree).
- ``l`` - distance between two points (arc length).
- ``n`` - number of points
- ``advised`` - (default=True) if True, compute an advised mark angle for each point
                        this is CPU-intensive.

OUTPUT:
a list of points

EXAMPLES::

    sage: from phystricks import *
    sage: C=Circle(Point(0,0),2)
    sage: pts=C.get_regular_points(0,90,1)
    sage: len(pts)
    4

The points in the previous examples are approximatively :
['<Point(2,0)>', '<Point(2*cos(1/2),2*sin(1/2))>', '<Point(2*cos(1),2*sin(1))>', '<Point(2*cos(3/2),2*sin(3/2))>']

def phystricks.src.CircleGraph.CircleGraph.get_tangent_segment	(		self,
			theta
	)

Return a tangent segment at point (x,f(x)).

The difference with self.get_tangent_vector is that self.get_tangent_segment returns a segment that will
be symmetric. The point (x,f(x)) is the center of self.get_tangent_segment.

def phystricks.src.CircleGraph.CircleGraph.get_tangent_vector	(		self,
			theta
	)

def phystricks.src.CircleGraph.CircleGraph.getPoint	(		self,
			theta,
			advised = True,
			numerical = False
	)

Return a point at angle <theta> (degree) on the circle. 

INPUT:
- ``theta`` - the angle given in degree.

def phystricks.src.CircleGraph.CircleGraph.graph	(		self,
			angleI,
			angleF
	)

Return a graph of the circle between the two angles given in degree

def phystricks.src.CircleGraph.CircleGraph.parametric_curve	(		self,
			a = None,
			b = None
	)

Return the parametric curve associated to the circle.

If optional arguments <a> and <b> are given, return the corresponding graph between the values a and b of the angle.

The parameter of the curve is the angle in radian.

def phystricks.src.CircleGraph.CircleGraph.put_arrow	(		self,
			arg,
			pw
	)

def phystricks.src.CircleGraph.CircleGraph.representative_points

(

self

)

def phystricks.src.CircleGraph.CircleGraph.xmax	(		self,
			angleI,
			angleF
	)

def phystricks.src.CircleGraph.CircleGraph.xmin	(		self,
			angleI,
			angleF
	)

def phystricks.src.CircleGraph.CircleGraph.ymax	(		self,
			angleI,
			angleF
	)

def phystricks.src.CircleGraph.CircleGraph.ymin	(		self,
			angleI,
			angleF
	)

Member Data Documentation

phystricks.src.CircleGraph.CircleGraph._equation

private

phystricks.src.CircleGraph.CircleGraph._numerical_equation

private

phystricks.src.CircleGraph.CircleGraph._parametric_curve

private

phystricks.src.CircleGraph.CircleGraph.angleF

phystricks.src.CircleGraph.CircleGraph.angleI

phystricks.src.CircleGraph.CircleGraph.center

phystricks.src.CircleGraph.CircleGraph.diameter

phystricks.src.CircleGraph.CircleGraph.linear_plotpoints

phystricks.src.CircleGraph.CircleGraph.pspict

phystricks.src.CircleGraph.CircleGraph.radius

phystricks.src.CircleGraph.CircleGraph.visual

---

The documentation for this class was generated from the following file:

• src/CircleGraph.py